System identification is the process of using measurements of the response of a system to infer the parameters that define its mathematical models. The identification of parameterized model classes and model parameters has several applications in structural mechanics, including operational condition assessment and management, improvement of design methods, design of experiments, structural control, and structural reliability applications, among others. With the increase in the design of engineering systems that exploit nonlinear phenomena the identification of nonlinear systems has gained significant attention in recent years. In structural systems typical sources of nonlinearity include large displacements, large deformations, material nonlinearity, boundary conditions, energy dissipation devices for vibration suppression, actuators, among others. In this research Bayesian methods are developed for the estimation of the parameters that define the models of nonlinear systems, and in the estimation of their dynamic response from measurements at limited spatial locations.
Identification of large-scale nonlinear structural and mechanical systems
Current research in system identification is centered in the development of methods scalable to large-scale nonlinear systems modeled using the finite element method. The scalability of nonlinear identification methods to high-order models is usually a limitation due to constraints in the identification methods themselves and/or the need of high computational resources. For this reason it is standard to rely on simplified reduced-order models with concentrated nonlinearity elements. However, the use of simplified models instead of the more advanced computational modeling tools currently available results in modeling errors that might compromise the predicting capability of the identified model.
This research aims to develop nonlinear identification methods with the capability to be successfully applied in high-order finite element models under different conditions, such as limited noisy measurements and lack of knowledge of the input excitations. Of special interest is the ability to identify model parameters under both material and geometric nonlinearity conditions. In particular geometric nonlinearity effects are usually neglected by current approaches, but these effects cannot be ignored in the modeling of flexible structures such as aircrafts wings.

Left: Experimental setup. Right: Model

Parameters posterior distributions

Yield displacement bivariate distributions

Related Publications
Erazo & Nagarajaiah. An offline approach for output-only Bayesian identification of stochastic nonlinear systems using unscented Kalman filtering. Journal of Sound and Vibration, 397(9), 222-240.
Erazo & Nagarajaiah. Bayesian Identification of an Adaptive Negative Stiffness System for Seismic Protection of Structures. Under Review.
Nonlinear dynamic response estimation using model-based stochastic filters
Estimation of the complete dynamic response of structural systems from spatially limited vibration response measurements has been a subject of recent interest in structural dynamics. Some applications include structural control, identification of model parameters, damage assessment and structural health monitoring. In this research model-based stochastic filters are developed to estimate the complete dynamic response of structural systems using incomplete noisy measurements. Model-based filters map the closed-loop (feedback) estimation problem to an equivalent open-loop (forward) problem that can be efficiently tackled directly in a finite element solver. Advantages of this strategy include reduced computational effort, and the ability to exploit the modeling capabilities offered by current finite element software.
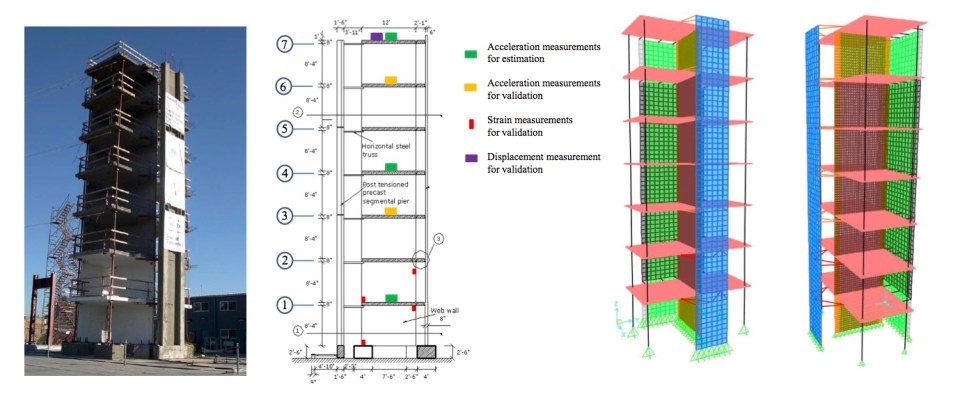
Experiment used in the validation of model-based filters. Left: 7-story full-scale structure. Middle: Measurements used for estimation and validation (assumed to be unknown). Right: Finite element model used to implement the filter.

A ground motion used in the experiment. VNUY transverse component of the 1971 San Fernando earthquake.

Roof acceleration estimate

Roof displacement estimate
Related Publications
Erazo & Hernandez (2016). High-resolution seismic monitoring of instrumented buildings using a model-based state observer. Earthquake Engineering and Structural Dynamics, 45(15), 2513-2531.
Erazo & Hernandez (2014). State Estimation in Nonlinear Structural Systems. In: Kerschen G. (eds) Nonlinear Dynamics, Volume 2. Conference Proceedings of the Society for Experimental Mechanics Series. Springer.
Identification of negative stiffness systems for seismic protection of structures
In this research nonlinear identification methods are applied in the context of a recently proposed adaptive negative stiffness system for seismic protection of structures. Adaptive systems are a class of passive devices that have the capability to modify their properties according to the response level experienced by a structure. Recently, a new adaptive system referred to as the adaptive negative stiffness (ANS) system was proposed. The ANS system has the ability to reduce both seismic response and base shear, while limiting inter-story drifts, and it consists of a negative stiffness device (NSD) and a viscous passive damper (PD).
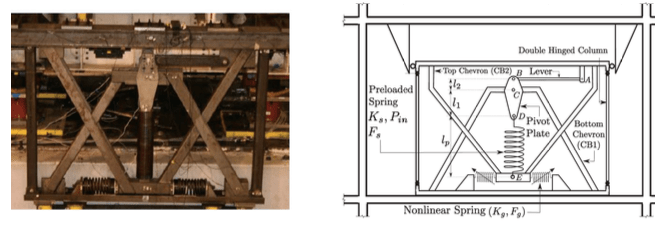
Negative Stiffness Device (Pasala et al., J.Str.Eng.)
The effect of the NSD is to assist in the motion of the structure reducing its effective lateral stiffness apparent weakening, a behavior that can be effectively modeled by adding ‘negative stiffness’ to the primary structure. Upon addition of the NSD the modified structure has a yield displacement that is considerably smaller than that of the primary structure, and in overall it behaves as an elastic bilinear system.
Bayesian methods are applied to estimate the parameters of a three story steel moment frame equipped with an ANS system using experimental data. The experiment was conducted in the shake table of the University at Buffalo – SUNY.



